
2009-9-8 16:51:33 上传
下载附件 (8.33 KB)


 附件: 4096魔方.GIF (2009-9-8 16:51:33, 8.33 KB) / 下载次数 267
附件: 4096魔方.GIF (2009-9-8 16:51:33, 8.33 KB) / 下载次数 267原帖由 乌木 于 2008-4-5 16:57 发表您说“二阶魔方的不重复的总状态数只有4*4*4=64种,……”,照您的想法,某一层可以转4下,其中有一下得到的是重复的态,您还可以继续“精简”呢。

 魔方只有三种状态:复原的,扣两秒的,和DNF的
魔方只有三种状态:复原的,扣两秒的,和DNF的





原帖由 joke 于 2008-4-5 19:09 发表 错了啊,二阶有8个小方块,先排列8小方块,然后每个小方块有3种方向,所以二阶: (8×7×6×5×4×3×2×1)×3×3×3×3×3×3×3×3=264539520种情况
原帖由 joke于 2008-4-5 19:21 发表 同理,三阶有8个角,12个棱角的不重复状态数就是二阶状态数264539520 12个棱,每个棱有2种状态所以,棱=(12×11×10×9×8×7×6×5×4×3×2×1)×(2的12次方)=1961990553600 然后,角和棱的情况是相互独 ...
原帖由 乌木 于 2008-4-5 20:12 发表注意,一般不大会多去探讨随机组装的总态数,而是探讨一个正确组装好了的魔方能够转出的总态数,您还要考虑色向关系的制约和消除同态--同一状态不同取向。也有的计算声明不消这种同态,则色向制约带来的 ...
原帖由 乌木 于 2008-4-5 20:12 发表注意,一般不大会多去探讨随机组装的总态数,而是探讨一个正确组装好了的魔方能够转出的总态数,您还要考虑色向关系的制约和消除同态--同一状态不同取向。也有的计算声明不消这种同态,则色向制约带来的 ...
原帖由 263442652 于 2008-4-5 20:11 发表实践比理论更重要...只要能够找到4097种变化,楼主的观点就不攻自破了.但是我却真正见过有人把所有的变化列举出来.所以就不要过早地否认楼主的观点和计算方法.事实胜于雄辩.如果嫌麻烦,可以先把65种二阶变化列举出来. ...



 附件: 楼主只取了4096个态.GIF (2008-4-7 01:05:43, 13.09 KB) / 下载次数 263
附件: 楼主只取了4096个态.GIF (2008-4-7 01:05:43, 13.09 KB) / 下载次数 263
 附件: 楼主只取了4096个态-2.GIF (2008-4-7 09:37:32, 4.08 KB) / 下载次数 234
附件: 楼主只取了4096个态-2.GIF (2008-4-7 09:37:32, 4.08 KB) / 下载次数 234


原帖由 乌木 于 2008-4-7 09:37 发表如果让中心块带有方向性,拆掉所有棱块和角块;或者所有的棱块和角块颜色没有区别,那样的魔方的状态数倒确实只有4096。各个中心块相互独立,故转动顺序对状态总数无影响。各个中心块方向变化是周期性的,故转动步数 ...
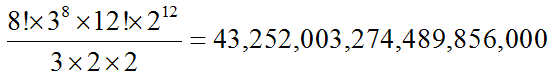
 附件: equation1.JPG (2008-4-9 17:54:07, 8.83 KB) / 下载次数 209
附件: equation1.JPG (2008-4-9 17:54:07, 8.83 KB) / 下载次数 209


 附件: 状态计算.jpg (2008-4-11 16:56:12, 63.56 KB) / 下载次数 152
附件: 状态计算.jpg (2008-4-11 16:56:12, 63.56 KB) / 下载次数 152原帖由 乌木 于 2008-4-12 00:45 发表不同的计算法不同,有的把同一情况的24种取向算作24种态,有的算作一个态,据不同要求而定。引用有关数据时只要关心一下有关前提即可。
原帖由 真知不易 于 2008-4-9 20:36 发表如果把魔方整体翻滚计算成不同的状态,不知道算不算是重复计算。

原帖由 senglin 于 2008-12-11 01:53 发表
我以为楼主说得有道理.
从哲学上说.一变为二,二变四,四变八,八变六十四,衍变于无穷.
眼光着眼于最后的变化,它就是很庞大的数字.
立足于各个点不同,状态数也就不同.

 附件: 4096魔方.GIF (2009-9-8 16:36:15, 8.33 KB) / 下载次数 133
附件: 4096魔方.GIF (2009-9-8 16:36:15, 8.33 KB) / 下载次数 133| 欢迎光临 魔方吧·中文魔方俱乐部 (http://bbs.mf8-china.com/) | Powered by Discuz! X2 |